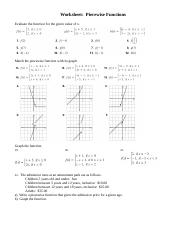
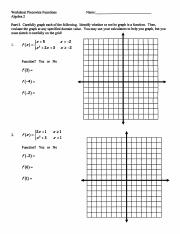
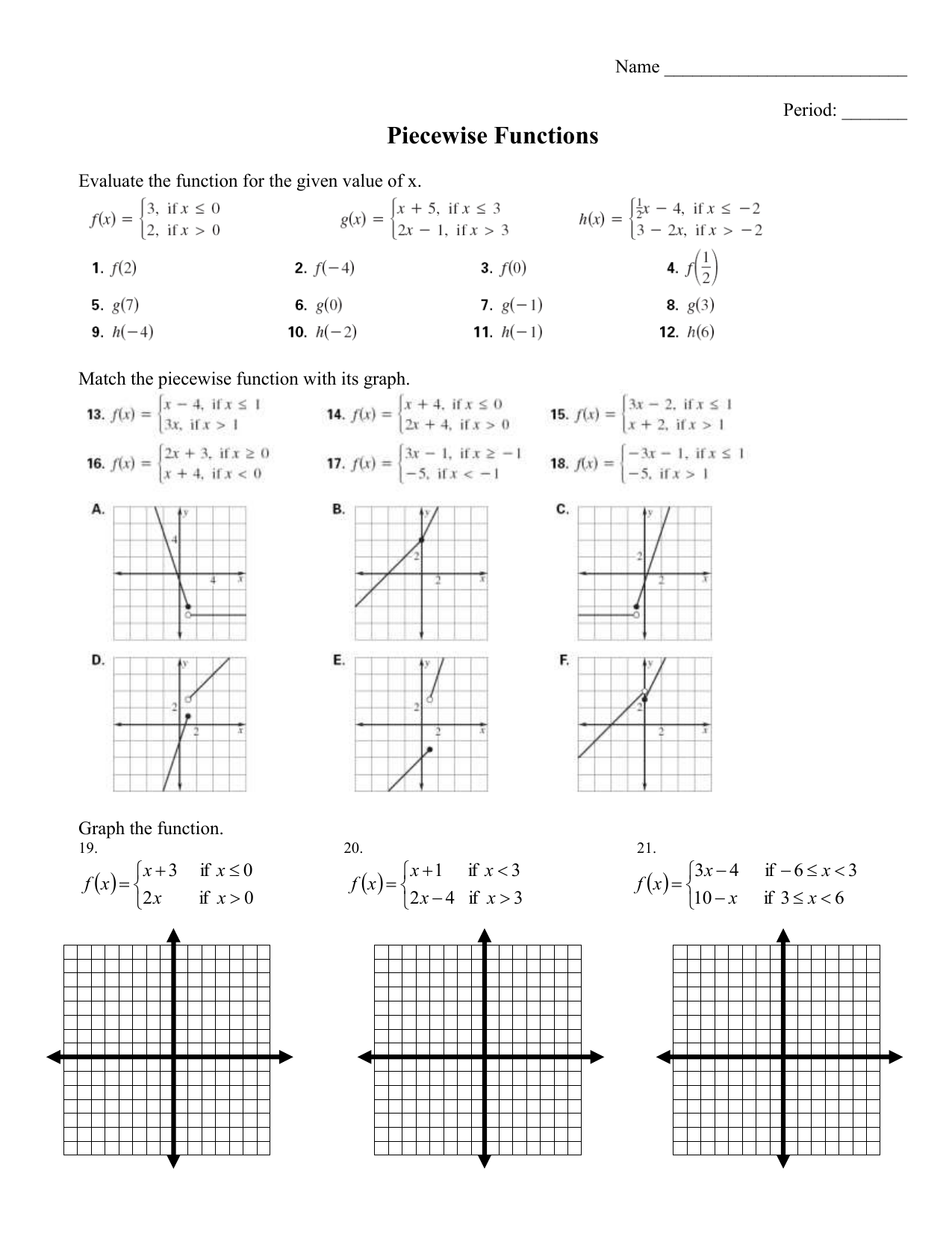
8 evaluating piecewise functions worksheet

Which of the following describes the domain of the piecewise function: [This is the piecewise function. Ignore the little question mark at the end, I don't know why that's there.](https://i.redd.it/waxg7j295mv71.gif) **Answer Choices:** (–∞, ∞) (–∞, 1) ∪ (1, ∞) (–∞, –2) ∪ (–2, 1) ∪ (1, ∞) (–∞, 1) ∪ (1, 2) ∪ (2, ∞) I think the answer is the third option: (–∞, –2) ∪ (–2, 1) ∪ (1, ∞), but I'm not completely sure. Would anyone be able to tell me what the correct answer is and why? While studying for an exam involving Fourier series, I have become a bit confused on how to interpret the domain of a piecewise function. I am supposed to find the Fourier series of a function defined as **f(x) = exp(x)** **for -π < x < 0, exp(-x)** **for 0 < x < π** . While attempting to confirm that this is an even function using the fact that even functions have the property f(-x) = f(x), I chose x = 1 . Plugging this in I get f(-(1)) = f(1) exp(-(1)) = exp(1) Clearly, this is ...

I have a piecewise function that varies based on an observation's decile rank. The decile is stored in a column of the dataframe. The calculation is a piecewise function such that: If the observation is below the first decile, it gets multiplied by 3000. If it is in the first decile, it gets multiplied by 2000. If its in the second decile, it gets multiplied by 1000. If it is in the third or higher decile, it gets multiplied by 0. Can one create a calculation that uses a dict?

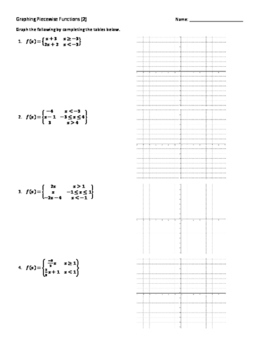
Evaluating piecewise functions worksheet

hey, so I've got this question, [https://i.imgur.com/aDuKCAx.png](https://i.imgur.com/aDuKCAx.png) via the chain rule, I think I can say h'(x) = f'(g(x))\*g'(x) and since the graph is piecewise, I can split it into 3 intervals: f(x) = 2x for 0 < x < 2 f(x) = -2(x-4) for 2 < x < 4 g(x) = 1-x for 0 < x < 4 which give derivatives of: f'(x) = 2 for 0 < x < 2 f'(x) = -2 for 2 < x < 4 g'(x) = -1 for 0 < x < 4 so h'(1)... So I've looked almost everywhere and I can't seem to figure out how to solve this problem. I read something about L'hôpital's rule, but I haven't learned this yet. Here's the problem (I had to put it in an image b/c stupid reddit formatting): http://imgur.com/a/RCyzw All I have so far is *lim as h→0 of [g(-1+h) - 1]/h* because when you input -1 into the function, you get 1 as the output. My question is how do I get rid of the god damn *g(-1+h)*? Let a: N -> N defined by a(n) = (n+1)/2 for odd n and a(n) = n/2 for even n, study the surjectivity of a. Let m in N, the equation m=n/2 has solution n=2m and the equation m=(n+1)/2 has solutions n=2m-1; since m is arbitrary, this holds for any m in N and hence any element m of the codomain N of a is mapped by at least one element of the domain N. My question is: was it enough to prove that one of the two equations m=n/2 or m=(n+1)/2 has always a solution to deduce the surjectivity of a? In...

Evaluating piecewise functions worksheet. Study the continuity of the function f defined as f(x,y)=exp{-1/\[y-(x+1)^(2)\]} if y<(x+1)^(2), or f(x,y)=0 if y>=(x+1)^(2). My try: for any real number t, the function is continuous in any point (x,y) different from (t,(t+1)^(2)) because it is composition of continuous functions or it is constant. Hence the only points to study are the points (x,y)=(t,(t+1)^(2)): now I would just say that, since there is no indeterminate form substituting, and exp{-1/\[y-(x+1)^(2)\]} -> +infinity as... Hi all, I am making a calculator in Desmos and I have run into this problem for the first time. [Link to Calculator](https://desmos.com/calculator/ior6vlggfe) I am trying to show certain points from a list based off of the piecewise function {l2 - round(l2) = 0: (l1,l2)}, but get an error saying “Cannot use a point and a number as the branches in a piecewise. Every branch must have the same type.” Is my goal even possible and if so, how can I fix this? Best, Pasta  https://preview.redd.it/xy4qd4b2m9571.png?width=543&format=png&auto=webp&s=74a88f095e0d5b0557eaaaf0f2195fb7aea29a26 [https://imgur.com/a/QWjfZ0l](https://imgur.com/a/QWjfZ0l) I'm confused why f(t) = f(t + 2\*pi) for all t, but there is t on defined on the interval 0 to 2\*pi? am I meant to simplify this function or write it in an alternative form?

link to the picture: [https://www.reddit.com/user/peasoup\_number/comments/nclfs5/my\_math\_equation/](https://www.reddit.com/user/peasoup_number/comments/nclfs5/my_math_equation/) Write a piecewise linear model for the following situation: Country Genovia has four income tax brackets. The tax rate for the first $22,000 of income is 10%. After that it increases to 18% for income up to $58,000; then 29% for income up to $118,000; and finally 38% for income over $118,000.  Here is my attempted solution with work: x<=$22,000, f(x)= 0.1x $22,000<x<= 58,000, f(x)= 0.1(22,000)+ 0.18(x-58000) f(x)= 2200+0.18x-10440 f(x)= 0.18x-8240 58000<x<=1... Solving for y worksheet solve for y. 7 y - x 1 8 y x 2 9 y 2x 1 10 I would first subtract two y from both sides to get a -3y on the right side. Pre Algebra Worksheets Linear Functions Worksheets Algebra Worksheets Writing Linear Equations Writing Equations Let a: N -> N defined by a(n) = (n+1)/2 for odd n and a(n) = n/2 for even n, study the surjectivity of a. Let m in N, the equation m=n/2 has solution n=2m and the equation m=(n+1)/2 has solutions n=2m-1; since m is arbitrary, this holds for any m in N and hence any element m of the codomain N of a is mapped by at least one element of the domain N. My question is: was it enough to prove that one of the two equations m=n/2 or m=(n+1)/2 has always a solution to deduce the surjectivity of a? In...

So I've looked almost everywhere and I can't seem to figure out how to solve this problem. I read something about L'hôpital's rule, but I haven't learned this yet. Here's the problem (I had to put it in an image b/c stupid reddit formatting): http://imgur.com/a/RCyzw All I have so far is *lim as h→0 of [g(-1+h) - 1]/h* because when you input -1 into the function, you get 1 as the output. My question is how do I get rid of the god damn *g(-1+h)*? hey, so I've got this question, [https://i.imgur.com/aDuKCAx.png](https://i.imgur.com/aDuKCAx.png) via the chain rule, I think I can say h'(x) = f'(g(x))\*g'(x) and since the graph is piecewise, I can split it into 3 intervals: f(x) = 2x for 0 < x < 2 f(x) = -2(x-4) for 2 < x < 4 g(x) = 1-x for 0 < x < 4 which give derivatives of: f'(x) = 2 for 0 < x < 2 f'(x) = -2 for 2 < x < 4 g'(x) = -1 for 0 < x < 4 so h'(1)...

Piece-wise Functions~ Evaluate & Graph~ 5 Practice ...

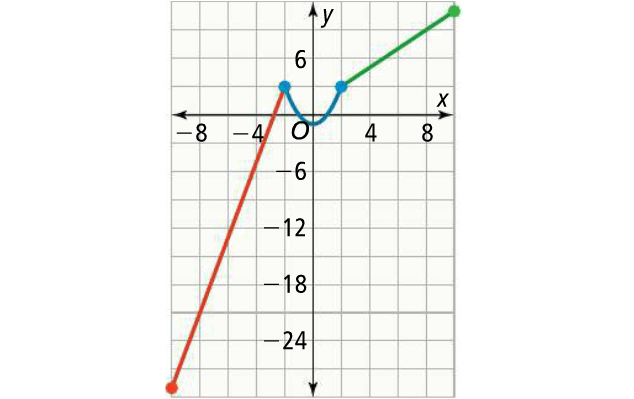
Piecewise Defined Functions Worksheet

Evaluating Functions Worksheet | Homeschooldressage.com

Obtaining Piecewise Functions from Graphs | Word problem ...

Piecewise Functions Activities with Googleâ„¢ Slides - Maze ...

Piecewise Functions Worksheet | Homeschooldressage.com

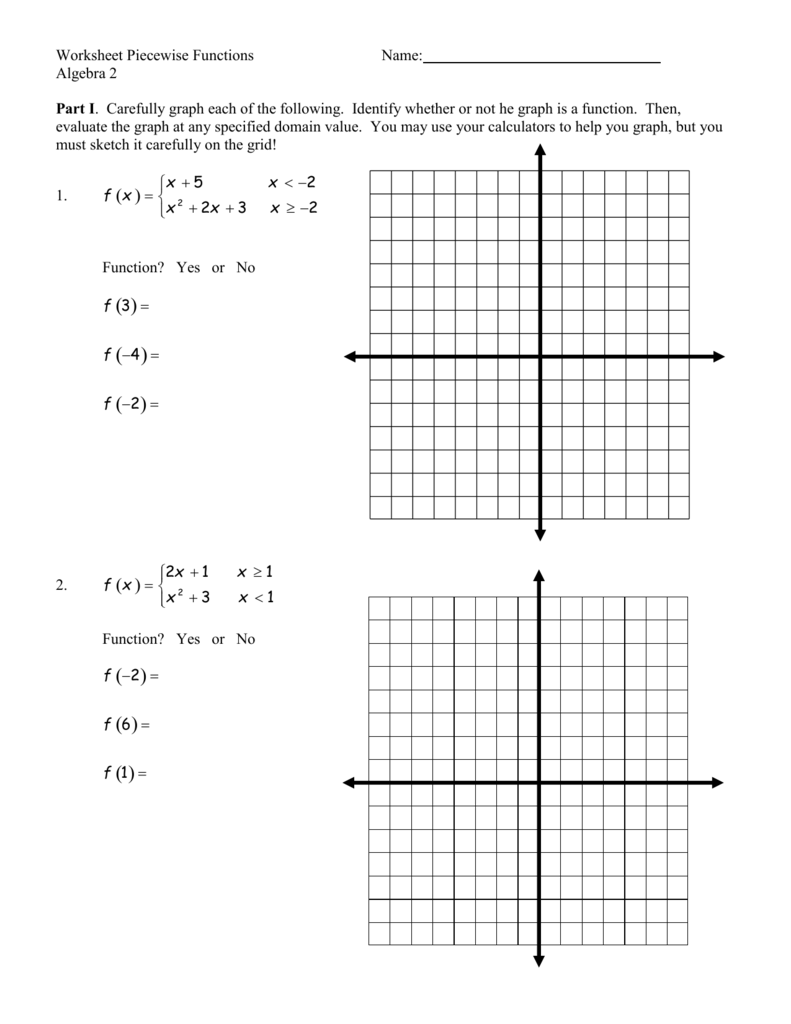
36 Evaluating Piecewise Functions Worksheet - Worksheet ...

Piecewise Functions Worksheet With Answers - Worksheet List

Worksheet Piecewise Functions

Colors celebration India

Evaluating Piecewise Functions Worksheet With Answers Pdf ...

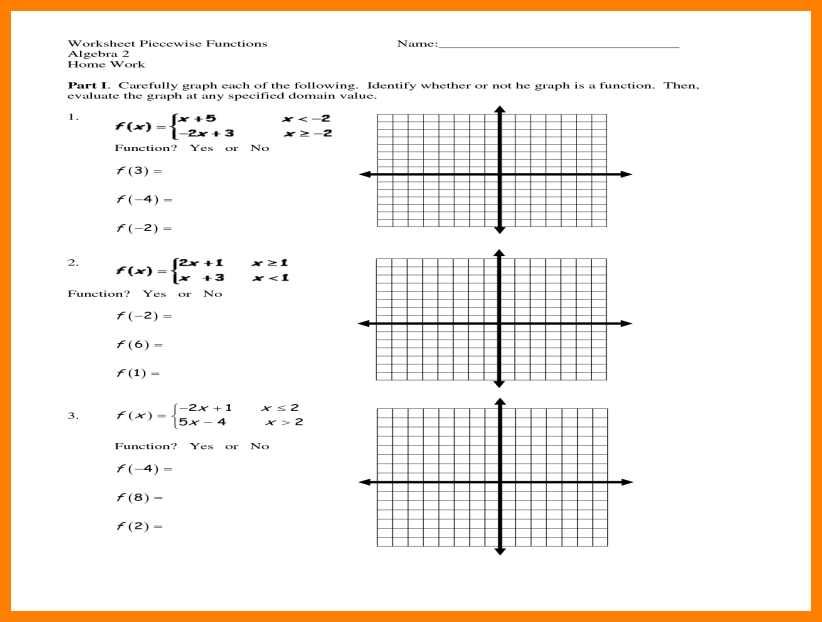
Worksheet Piecewise Functions Algebra 2 - Worksheet List

WS Piecewise Functions.doc - Worksheet Piecewise Functions ...

15 Best Images of Evaluating Functions Worksheets PDF ...

33 Piecewise Functions Word Problems Worksheet With ...

Evaluating Piecewise Functions FUNsheet by Common Core Fun ...

Evaluating Functions Worksheet | Homeschooldressage.com

City Strolling. Finding different viewpoints of common drinking spots.

Evaluating Piecewise Functions Worksheet Pdf - best worksheet

Math 2 Piecewise Functions Worksheet 2 Answers - algebra 2 ...

Maths homework / worksheet

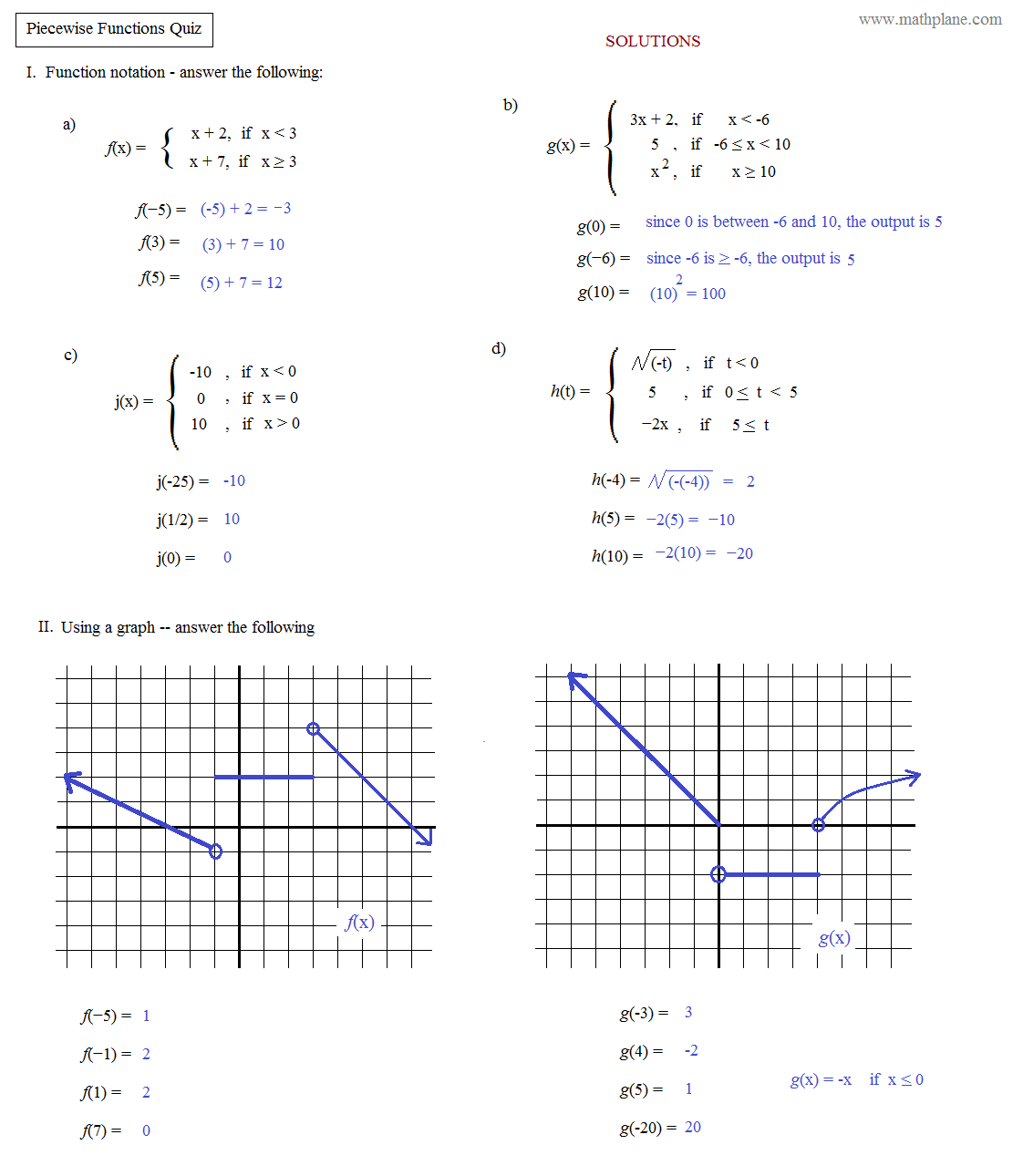
Piecewise Functions Evaluate Worksheet Answers | Free ...

15 Best Images of Evaluating Functions Worksheets PDF ...

Evaluating Piecewise Functions Worksheet With Answers Pdf ...

15 Best Images of Evaluating Functions Worksheets PDF ...

32 Algebra 2 Yl 44 Graphing Piecewise Functions Worksheet ...

Evaluating Piecewise Functions Worksheet With Answers Pdf ...

Evaluating Piecewise Functions FUNsheet by Common Core Fun ...

Newborn Baby Having Lungs and body temperature checked: doctors listen to a newborn's lung function while checking the body temperature in an operating room. A depiction of childbirth.